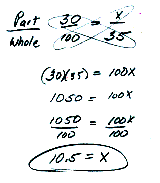Learning Activity 5-D-2: Applets

I like the Shape Sorter game on the illuminations website, as indicated below.  I was immediately drawn to the game because I am currently teaching a geometry unit; thus, the game has current relevance.  One of things I like most about the game is that it is very comprehensive.  For example, the game encompasses everything from polygon characteristics, to symmetry, angles, and Venn Diagrams.  Students select their own Venn Diagram categories from a long list of options; therefore, I also like the fact that the students are in control of their own learning.  I can definitely see myself using the applet as an assessment tool in the near future.  Since the applet displays the correct & incorrect responses at the end of each round, I would also have my students write about why some of their answers were wrong.

http://illuminations.nctm.org/ActivityDetail.aspx?ID=34

 

Learning Activity: 5-A-4 Evaluating our Definitions: Equations and Functions

After reviewing my classmate’s posts on functions and equations, I noticed that many of the definitions and examples were similar.  Other than having different semantics, we all pretty much created the same definitions.  If I were to alter one thing about my definition, however, I would write more about the patterns that are created by functions, and mention that equations don’t have to have variables on each side of the equation.  Although I provided examples that illustrated this, I didn’t mention it in my definition.

To evaluate whether my students grasp the difference between the two, I would have them write examples of equations and functions in their journals.  Subsequently, I would have them create a Venn Diagram to organize their data, and require them to compare and contrast the two.  I would allow them to use any resource they would like to create a multitude of examples.

Learning Activity 5-3-A: My Definition of Equations & Functions

Equation: An equation is a numeric or algebraic number sentence that is made up of two expressions: one on each side of an equal sign.  Equations must maintain their balance on each side of the equal sign.

Examples of Equations:

Y = 2r + 7                   76 = 14/X                      7(4 + 5) =

Function: A function is an algebraic equation that has two variables or missing values: one on each side of an equal sign.  When one of the variables is replaced with a numeric value, the equation can be solved, and there is an output for the other variable.

The links and activities below are supplementary resources that reinforce equations and functions.

 

 

 

 

 

 

 

 

Examples of Functions:  

f(x) = 3 + 6x       f(x) = 54x + 17       f(x) = 87 – 54x

Defines Functions; Provides Examples & On-line Practice.

http://www.studyzone.org/testprep/math4/d/functiontable4l.cfm

Defines Functions; Provides Examples; Discusses Variables and Domains & Ranges; Graphing Functions & Function Tables.

http://www.ehow.com/about_5431722_math-function-table.html

Comprehensive Review of Linear Equations, Including On-Line Practice, Tests & Illustrations.

http://www.mathsisfun.com/equation_of_line.html

Comprehensive Video That Reviews  A Variety Of Different Forms Of Simple Linear Equations.

http://player.discoveryeducation.com/index.cfm?guidAssetId=9D45C18B-ECE5-4B1B-BFB9-D8A56F3CCCFA&blnFromSearch=1&productcode=US
                                                                        

Journal Activities

1.  Write about a real-world situation that has a constant rate of change and a Y-intercept.  For example,  NYC cabs charge .45 per mile and an initial fee of $3.00.

1a. Create an equation that represents your example.

2. Create your own pattern of six numbers, along with a concrete visual of your pattern.  Describe the rule associated with your pattern.

Learning Activity 5-B-1: The Magic of Proportions

In 2010 I had the opportunity to travel to Moscow, Russia where the currency is the Russian Ruble.  29.93 Russian Rubles is equivalent to 1 US Dollar; therefore, every time I made a purchase, I converted the Russian Rubles to US Dollars to understand the real value of my purchases.  For example, if a large bag of potato chips had a price tag of $89.73, I used my knowledge of proportions to convert the price to US Dollars.  The example below illustrates how I used proportional reasoning to convert the prices.

Example #1

If 1 US Dollar = $29.93 Russian Rubles, what is the dollar value of a $89.73 bag of potato chips?

Step 1

Create a ratio, or part to part relationship.

$1 US Dollar/$29.93 Russian Rubles

The ratio above means that for every $1 US Dollar, there are $29.93 Russian Rubles. 

Step 2

Create another ratio, or part to part relationship, that includes the missing value.

C/$89.73 Russian Rubles

The ratio above asks that question: how many US Dollars are there for every $89.73 Russian Rubles?

Step 3

Make the two ratios equivalent so they become a proportion.

$1 US Dollar/$29.93 Russian Rubles = C/$89.73 Russian Rubles

The proportion above asks the question: if $1 US Dollar represents $29.93 Russian Rubles, how many US Dollars represent $89.73 Russian Rubles?

Step 4

Cross multiply on both sides of the proportion.  For example, $29.93 Russian Rubles times C, and  $1 US Dollar times $89.73 Russian Rubles.  The cross multiplication produces the following equation:

$29.93(C) = $89.73

Step 5

To solve the equation, isolate the variable, C, by performing the inverse, or opposite, operation.  The inverse of multiplying by $29.93 is dividing by $29.93.

$29.93(C)/$29.93 = 1(C)

Step 6

Since we divided by $29.93 on the left side of the equation, we must also divide by $29.93 on the right side of the equation, because equations must maintain their balance.

$89.73/$29.93 = $2.99

Final Answer

1C = $2.99

The final answer means that $89.73 Russian Rubles is equivalent to 2.99 US Dollars.  Thus, a large bag of potato chips that are $89.73 Russian Rubles have the same value as 2.99 US Dollars.

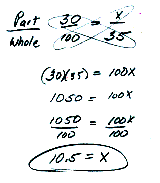
Example #2

The school’s planning committee has decided to make and purchase Country Time Lemonade for the student’s Valentines Day party.  One 82.5 oz canister of Country Time serves 136 people.  How many canisters of lemonade are needed to serve approximately 300 people/students?

Step 1

Create a ratio, or part to part relationship.

One Canister (82.5 oz)/136 Students (Servings)

The ratio above means that for every one canister of 82.5 oz lemonade, 136 students can be served.

Step 2

Create another ratio, or part to part relationship, that includes the missing value.

C/300 Students

The ratio above asks that question: how many canisters of lemonade are needed to serve 300 students?

Step 3

Make the two ratios equivalent so they become a proportion.

1 Canister/136 Students = C/300 Students

The proportion above asks the question: if 1 Canister of lemonade serves 136 students, how many canisters are needed to serve 300 students?

Step 4

Cross multiply on both sides of the proportion.  For example, 136 Servings times C, and  1 Canister times 300 students.  The cross multiplication produces the following equation:

136(C) = 300

Step 5

To solve the equation, isolate the variable, C, by performing the inverse, or opposite, operation.  The inverse of multiplying by 136 is dividing by 136.

136(C)/136 = 1(C)

Step 6

Since we divided by 136 on the left side of the equation, we must also divide by 136 on the right side of the equation, because equations must maintain their balance.

300/136 = 2.20

Final Answer

1C = 2.2 of a Canister, or 3 Whole Canisters

The final answer suggests that 3 Canisters (82.5 oz) of Country Time Lemonade are needed to serve 300 students.  Since the final answer, 2.20, has a remainder, it means that 2 Canisters are not enough; therefore, an additional Canister is need.

Learning Activity 4-C-1: Non-Linear Pattern Web Quest

For this Learning Activity, I conducted a web-quest on “Fractals and Nature.”  I chose this particular web-quest because, although I’ve heard of fractals before, all I really knew about them was that they were patterns.  I didn’t know the formal definition of the word, nor did I know how the patterns were created.  Since I started this process with a clean slate, everything I learned was entirely new to me.  For instance, one of the most fascinating things I learned was that fractals can be computer-generated with the appropriate software and mathematical formula.  I also found it interesting that some artists make a living from drawing fractals, whereas others are paid to create computer-generated fractals and set them to music.  Initially, many of the websites I visited provided very detailed and mathematically confusing definitions of fractals.  However, I found the links below to be very helpful and simplistic.

http://player.discoveryeducation.com/index.cfm?guidAssetId=710F2EBB-27F0-439A-AB92-ECFD1F6879D1&blnFromSearch=1&productcode=US

http://tiger.towson.edu/~gstiff1/fractalpage.htm

Here are a few fractal pictures I found particularly striking.  From left to right, the first illustration is a mountain range found in nature, the second is a fractal that was created on someone’s back as a result of being struck by lightning, and the last fractal was found by slicing a head of cabbage.

At my school we have a large student population of Caribbeans, Caribbean Americans, and African-Americans.  Thus, I think it would be nice to have students identify fractal patterns within the various braided hair styles many of them wear to school.  Student’s could also find braided fractal patterns on-line, or in print.

In my home, I have non-linear patterns on my curtains, counter-top, and within a crocheted bed spread I am in the process of making.  In my classroom, there are non-linear patterns on my bulletin board, based on the way the student’s work is staggered and displayed, and there are graphing posters that are displayed throughout the room that have non-liner patterns, as well.

In addition to conducting a web-quest on “Fractals and Nature,” I also conducted a web-quest on “Fibonacci and Prime Numbers.”  Although I was quite familiar with prime numbers, I was not so familiar with Fibonacci’s Sequence, although I’ve heard about it before.  Initially, I didn’t know how to solve the sequence, until I analyzed it thoroughly.  However, I did eventually notice that two consecutive numbers could be added together to  obtain the third number.  Another concept I learned was that within any group of three numbers, the first and the third number could be multiplied, and the middle number could be squared; the difference between the two numbers is always one.  With specific regard to prime numbers, I learned that every number in the sequence is either prime, or is the product of the prime factorization of the number.  For example, although the number eight is not prime, it is the product of four and two, and two is a prime factor of eight.  The websites that assisted me with understanding this new insight are listed below.

http://player.discoveryeducation.com/index.cfm?guidAssetId=80B45D3D-F904-4560-BE00-BA479DF7511E&blnFromSearch=1&productcode=US

http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibmaths.html#primefactor

Within the school setting, students could identify Fibonacci’s Sequence on the piano keys in the music department, or they could use manipulatives to re-create the production of the rabbit pairs.  Within my home, I could probably find Fibonacci’s sequence applied in some of the knitting & crochet books I have; especially those patterns that have petals and spirals.  The photos below are striking photos of Fibonacci’s Sequence found in architecture, nature, needle work and the human body.

 

Learning Activity 4-A-2: Working with the Definition of Linear Patterns

Non-Traditional Patterns (Formal Definition): Patterns that do not follow a repetitive format.

Linear Patterns (Kid-Friendly Version): Patterns that have constant rates of change.  The patterns may constantly increase, constantly decrease, or constantly stay the same.  For example,  the amount of money one makes for babysitting may constantly increase by $10 every hour; the temperature may constantly fall/decrease by -5 every hour; Kim may constantly receive an allowance of $20 each week, no matter how many chores she has or has not completed.

Linear Patterns (Formal Definition): Linear patterns are patterns that have the same distance between each term; the pattern repeats indefinitely along a line.

Definition Comparisons:

• My definition references constant rates of change, while the formal version references distances between terms.
• My definition mentions that the constant rate may be positive, negative, or the same; the formal definition has no mention.
• We both mention that linear patterns look like straight lines.
• The formal definition makes reference to the line being indefinite; mine does not.
• Both definitions make reference to the pattern being repetitive or constant.
• I provided examples of real-world constant rates of change, even although it wasn’t a requirement.

I think students can learn the formal definition of linear patterns by providing them with visual representations first.  For example, if students were provided visuals of linear patterns that demonstrated positive rates of change, negative rates of change, and a zero rate of change for X and Y, I am confident they could work backwards to  come up with their own definition of a linear pattern.  Once they analyze the data and see the patterns for their self, the formal definition would make more sense, and it wouldn’t have to be memorized.  Rather, the abstract definition would be  more easily understood as a result of the prior visual analysis and informal interpretation.

 

 

My Reflection on Math Myths

As a math student, I believed the myth that suggested that there was only one way to calculate  a problem.  For example, as mentioned previously, my teachers would give examples, and provide us with the steps for solving the problem.   Therefore, the only strategies I knew were the ones that he/she placed on the board.  If an alternative strategy wasn’t on the board, in my notebook, or in the textbook, I assumed an alternative didn’t exist.  In my mind, if an alternative strategy did exist, someone would have told me or showed me.

Unfortunately, I believed this myth until I became a teacher and started taking graduate classes in math education.   As a graduate student, I noticed that my classmates didn’t always perform the same calculations to get the same answers.  Additionally, once I became a teacher, I was encouraged to allow my students to investigate and discover, rather than “show and tell,”  as I was taught.  As a teacher who now knows the truth, I encourage my students to discover rules and methods on their own, prior to teaching and showing them what I know.  Similarly, I also use various questioning techniques such as, “did any one do anything differently?,” “can you think of another way to get the same answer?,” “what else could you do?”

A second myth I also believed pertained to the “good students” ability to calculate mental math.  For example, I believed that if you were able to calculate mental math relatively quickly, than you were beyond smart; you were in the “really smart” category.  It wasn’t until I was in college that I realized that there were other students in my class who were smart, who didn’t necessarily apply speed and mental calculations to get the answer.  Fortunately, I happened to be one of those students; however, I was more passive and methodical when it came to math.  I was the one who read the question three times, and checked my work three times, while the “really smart”  students were blurting out answers they calculated in their heads.

This myth could easily be perpetuated if teachers don’t take the time to dialogue with the students who work at a slower pace.  I always try to encourage my students to take their time and stay focused; I want them to stay committed to their task, without worrying about another student’s pace.  Therefore, I have to constantly remind them that math is not a race; the goal is understanding, not finishing first.  As an educator, it’s important to nurture my student’s sense of accomplishment, so they can see for themselves that they can accomplish the same goal, although it may be at a slower pace.  Positive reinforcement like a simply high-five or pat on the back can go a long way, and encourage them to keep trying.

Learning Activity 4-C-3: Translating Pattern Naratives into Formal Language

• The number one is always the first and the last number in the row.
• The number one is the only number in both of the outer diagonals.
• There are counting numbers in the second diagonal from left to right and right to left (1,2,3,4,5,6,7 etc).
• The second number in each row is also the second to the last number in each row.
• Each diagonal from left to right corresponds with a diagonal that goes from right to left; they have the same numbers in their list because the triangle is symmetrical.
• The triangle is equilateral.
• The sum of the two consecutive numbers one row above is the answer to the number one row below.   
• The sum of the digits in each row is obtained by doubling the sum of the digits in the previous row.
• Only positive numbers are included in the triangle.
• Some rows and diagonals contain all odd numbers.
• The digits in each row are powers of 11.

3-E-2 Reviewing the Puma Site

After reviewing the Puma Site examples, I found the Dream Job activity to be the most appealing.  Although the activity is designed for high school students, the lesson could be tweaked to accommodate my 6th & 7th graders.  I am confident my students would enjoy this activity because it involves money, which would pique their interest.  Additionally, I also think they would enjoy signing their first work-related contract.

I like that the activity addresses many components of number sense.  For example, it requires students to add, multiply, estimate, understand place value and the magnitude of numbers, as well as organize data.  If I were to tweak the lesson, I would delete the values that are within the weekly templates, and require students to calculate them on their own.  Although my students wouldn’t entertain the questions pertaining to geometric progression,  they could definitely answer #1-#4 on the questionnaire.  Since this activity is time-consuming, I would encourage students to work on it whenever they finished their classwork early; it would also be a great component for a vacation packet.  Another alternative would be to assign different groups of students to calculate particular weeks.  For example, I have six groups of four in my classroom; thus, Group 1 could calculate Weeks 1-5; Group 2: Weeks 6-10, Group 3: Weeks 11-15 etc.  There are a number of modifications that could be made to make the lesson less tedious and more appealing to grades 6-8.  I will probably include it in my vacation packet for winter recess.

3-D-2: Inverse Properties

The Additive Inverse Property suggests that any number added to its opposite number is equal to zero.  For instance, in the example, 9 + (-9), -9 is the opposite of 9.  Thus, when the numbers are added together, they cancel each other out, and the sum is zero. 

Here are a few more examples:

28 + (-28) = 0

16y  + (-16y) = 0

-220b + 220b = 0

5,658 + (-5,658) = 0

3/4 + (-3/4) = 0

The Multiplicative Inverse Property is very similar to the Additive Inverse Property.  For example,  this property suggests that any number multiplied by its reciprocal is one.  To find the reciprocal of a number, make the numerator the denominator, and the denominator the numerator.  For example, the reciprocal of 5/3 is 3/5.  In the case of a whole number, the denominator is always one, so the reciprocal of 16 or 16/1 is 1/16.  In simple terms, to find the reciprocal, you must “flip” the fraction up-side down.  Once you write the reciprocal and multiply straight across, you will get a fraction that has the same number in the numerator and the denominator.  Thus, they cancel each other out, and the quotient is one.

Here are a few more examples:

3/22 x 22/3 =  66/66 = 1

30 x 1/30 = 30/30 = 1

911/1 x 1/911 = 911/911 = 1

87r/10 x 10/87r = 870r/870r = 1

-2/3 x 3/-2 = -6/-6 = 1